机器学习

1 课程定位

科学：是什么？为什么？

技术：怎么做？

工程：如何做的多、快、好、省

应用

机器学习这门课程：以科学、技术为主。

2 机器学习概念

经典定义：利用经验改善系统自身的性能。(Tom Mitchell 的《Machine Learning》教材)

• Tom Mitchell 的《Machine Learning》（1997）中提出：“A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.”（即“通过经验改进性能”的核心思想）。

随着该领域的发展，目前主要研究智能数据分析的理论和方法，并成为智能数据分析技术的源泉之一！

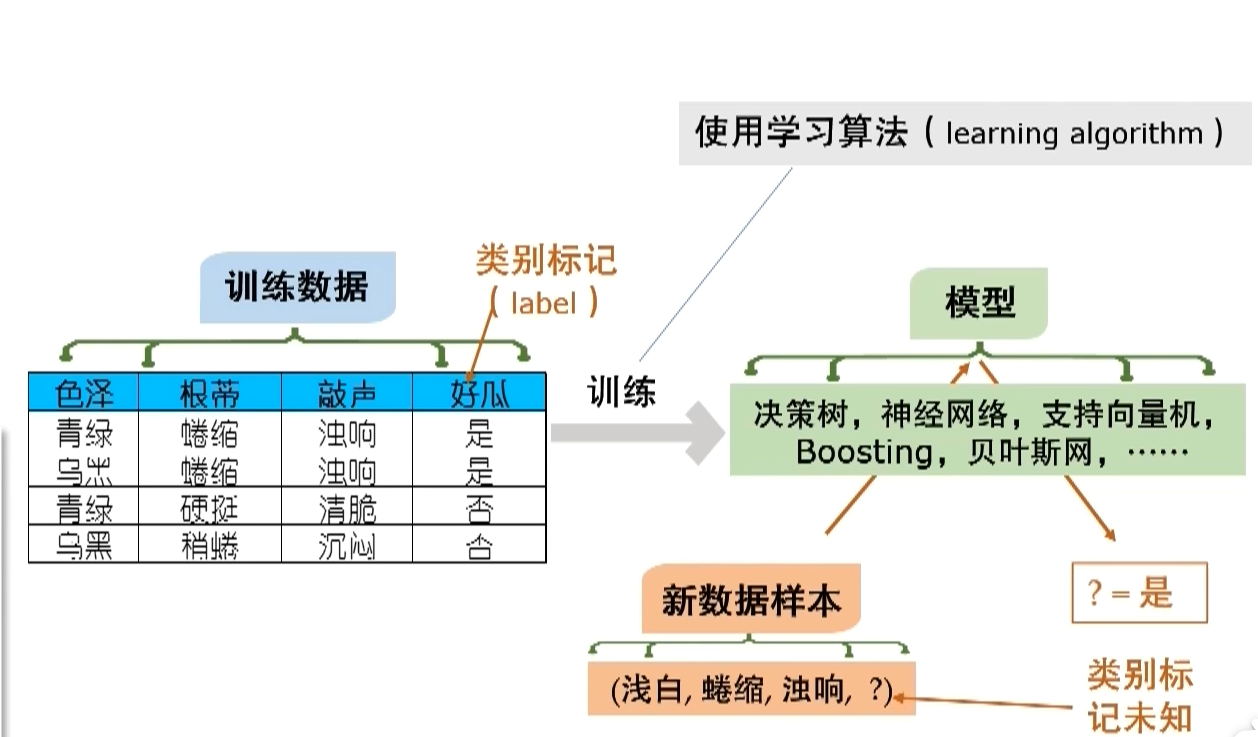
3 典型的机器学习过程

4 机器学习计算学习理论

PAC是Probably Approximately Correct 的缩写，中文译为”概率近似正确”。这是计算学习理论中的一个重要框架，由Leslie Valiant在1984年提出。该理论为机器学习算法的有效性提供了严格的数学定义和分析工具。

$$P(|f(\boldsymbol{x}) - y| \leq \epsilon) \geq 1 - \delta$$

公式说明：

$$P: 概率 (Probability)\\ f(\boldsymbol{x}): 学习算法得到的模型在输入 \boldsymbol{x} 上的预测值\\ y: 真实标记\\ \epsilon: 误差范围 (Error parameter)\\ \delta: 置信度参数 (Confidence parameter)，1-\delta 即为置信度\\$$

4.1 公式问题

问题1：为什么不追求？

$$\epsilon = 0$$

问题2：为什么是个概率？为什么不能绝对能拿到它？

机器学习通常在解决什么问题呢？是解决一个高度不确定性，高度复杂性，而且你甚至不知道怎么去做它！

从知识层面角度：

当我们的知识不能给我们准确结果的时候，我希望通过数据中找到答案，但是这个答案并不可能是100%正确的，因此是一个概论值！

从计算的角度：

在计算机学科比较关心的问题是：

$$P?=NP$$

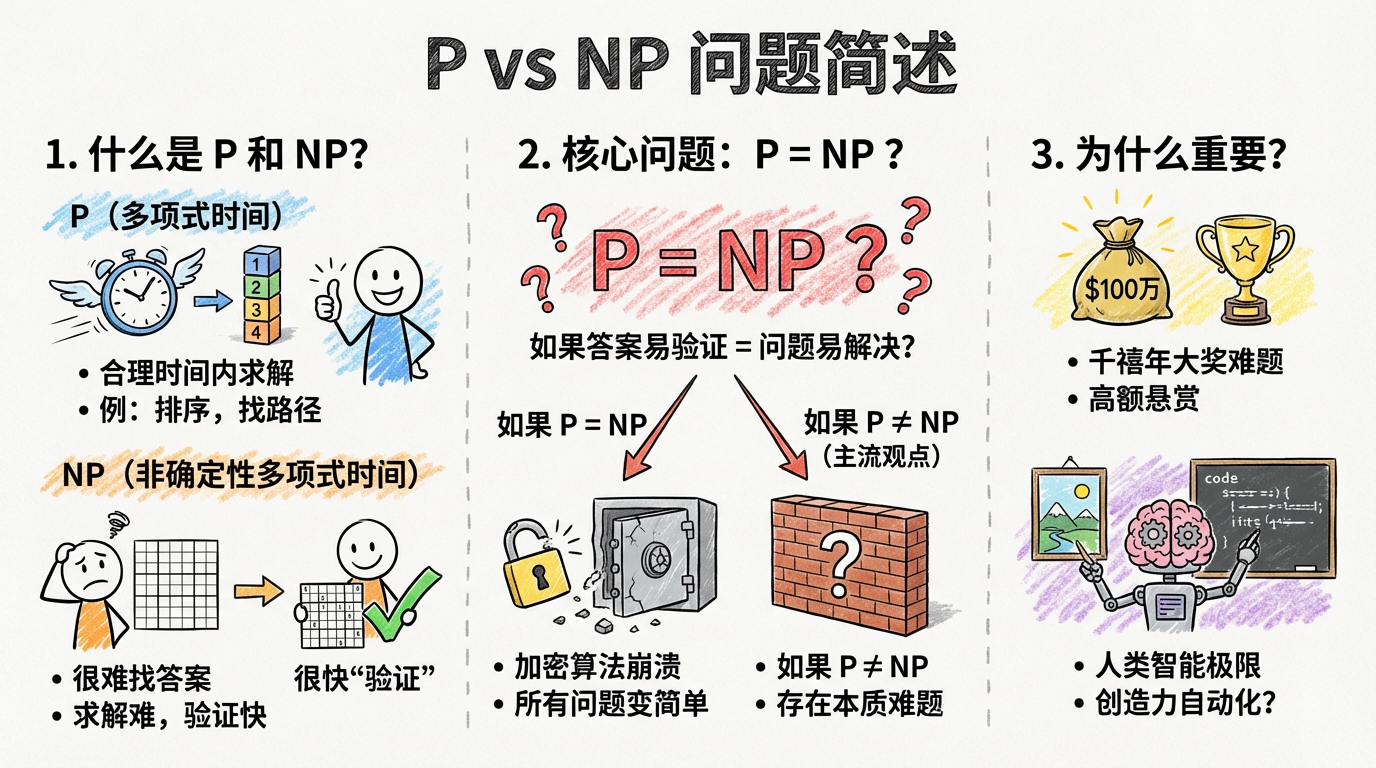
1. 什么是 P 和 NP？

这是衡量算法复杂度的两个核心类别：

• P (Polynomial time - 多项式时间)： 指的是那些可以在“合理的时间内”找到答案的问题。比如：对一组数字进行排序、查找地图上的最短路径。计算机处理这类问题非常高效。

• NP (Nondeterministic Polynomial time - 非确定性多项式时间)： 指的是那些虽然很难找答案，但如果给你一个答案，你可以很快“验证”这个答案对不对的问题。

  • 例子： 数独游戏。自己解开一个高难度的数独可能要很久，但如果别人填好了给你，你扫一眼就能确认每行每列是否符合规则。

2. 这个问题的核心是什么？

公式中的问号表达了一个终极疑问：“如果一个问题的答案可以很快被验证，那么它是否也能很快被解决？”

• **如果 **

  $$P = NP$$

  ：意味着所有容易验证的问题都容易解决。如果这被证明是真的，现有的很多加密算法（如网银、比特币背后的加密逻辑）将瞬间失效，因为计算机能轻易破解它们。

• **如果 **

  $$P \neq NP$$

  （目前大多数科学家倾向于这个结论）：意味着世界上确实存在一些本质上“难解”的问题，即便验证它们很简单。

3. 为什么它如此重要？

• 地位：它是克雷数学研究所公布的七个“千禧年大奖难题”之一，悬赏奖金为 100 万美元。
• 意义：它不仅是数学问题，更关乎人类智能的极限。如果 P=NP，很多看似需要创造力的任务（比如写代码、证明定理、进行复杂的科学发现）都可以被算法高效地自动完成。

4.2 总结

PAC 理论实际上是在承认现实世界复杂性的前提下，为“计算机能否在有限时间内学会某个知识”寻找一条出路。

PAC 理论通过容忍微小的误差（$\epsilon$）和失败概率（$\delta$），确保了机器学习任务能够在有限（多项式）时间内计算完成，而不至于陷入追求绝对完美带来的计算泥潭。

在机器学习中，以很高的概率得到很好的模型！

4.3 独立同分布

独立同分布（Independent and Identically Distributed，简称 i.i.d.）是机器学习和 PAC 理论得以成立的基石假设。

可以用一句话来直观理解：训练数据和未来的测试数据，必须是“用同样的规则、在互不干扰的情况下”产生的。

具体拆解如下：

1. 独立 (Independent)

• 含义： 样本之间没有关联，谁也不影响谁。
• 例子： 你抛 10 次硬币，第 1 次的结果不会影响第 2 次。
• 在机器学习中： 我们抽取的每一个训练样本（比如一张猫的照片）都应该是随机且独立的，不能因为抽到了 A 就导致抽到 B 的概率变大。

2. 同分布 (Identically Distributed)

• 含义： 所有样本都来自同一个“大母体”（同一个概率分布）。
• 例子： 你这 10 次抛的必须是同一枚硬币。如果你前 5 次用正常的硬币，后 5 次换成了两面都是正面的灌铅硬币，那就不是同分布。
• 在机器学习中： 训练集和测试集必须来自同一个世界。如果你训练时给模型看的是“北京的交通图”，测试时却考它“东京的交通路况”，模型就会失效，因为分布变了。

为什么 PAC 理论必须要求 i.i.d.？

回到之前的那个 PAC 公式：

• 如果没有“同分布”： 你在训练集上学到的规律f(x)在测试集上根本没用，因为“考试大纲”变了，概率预测也就失去了意义。
• 如果没有“独立”： 样本之间如果存在强耦合（比如全是重复数据），那么样本量再大也无法代表真实的规律，学习就会产生严重的偏差。

形象比喻： 你要通过尝一口汤来判断一锅汤咸不咸。

• 同分布： 你得把汤搅匀了（确保每一口都代表整锅汤）。
• 独立： 你得随机喝一口，而不是盯着放盐的地方连续喝好几口。

4.4 突破独立同分布

突破“独立同分布 (i.i.d.)” 假设不仅是当前机器学习的前沿，甚至可以被认为是通往“通用人工智能 (AGI)”的必经之路。

在学术界和工业界，这个研究方向通常被称为 “分布外泛化 (Out-of-Distribution Generalization, 简称 OOD)” 或 “鲁棒性 (Robustness)” 研究。

为什么要突破它？因为在现实世界中，i.i.d. 几乎是不存在的。以下是目前最前沿的几个研究方向：

1. 迁移学习与领域自适应 (Transfer Learning / Domain Adaptation)

• 问题： 训练数据在 A 场景（如白天拍摄的自动驾驶数据），测试在 B 场景（如雨天或夜晚）。
• 突破： 研究如何让模型将在 A 领域学到的知识，“迁移”到分布完全不同的 B 领域。

2. 连续学习 / 增量学习 (Continual Learning)

• 问题： 传统的 i.i.d. 假设数据是一次性给齐的。但在现实中，数据是像流水一样过来的，且每个阶段的主题都不同。
• 挑战： 灾难性遗忘 (Catastrophic Forgetting)。模型学了新知识（新分布），就会把旧知识（旧分布）忘光。研究前沿是如何让模型像人一样，在非 i.i.d. 的数据流中持续积累知识。

3. 因果推理 (Causal Machine Learning)

• 核心逻辑： 这是目前最深刻的突破方向。i.i.d. 依赖的是相关性（看到云觉得会下雨），而因果推理追求的是本质规律（云是水蒸气凝结，这在任何地方都成立）。
• 突破点： 图灵奖得主 Judea Pearl 和 Yoshua Bengio 等大牛都在推动：如果模型能抓住数据背后的“因果链条”，那么即便数据分布变了（非同分布），规律依然有效。因果性是抗衡非 i.i.d. 的终极武器。

4. 联邦学习中的 Non-IID 问题 (Federated Learning)

• 场景： 数据分布在千万台手机上，每个用户的使用习惯（分布）完全不同。
• 突破点： 如何在不把数据汇总的情况下，从千万个完全不同的非同分布数据源中练出一个通用的强大模型。

5. 大模型 (LLM) 的“暴力破解”

• 现状： GPT 等大模型通过海量的数据（几乎吞下了整个互联网），实际上是在试图用“覆盖全集”的方式来逼近 i.i.d.。
• 逻辑： 当你的训练集足够大，涵盖了几乎所有的场景时，原本属于“分布外”的东西也就变成了“分布内”。

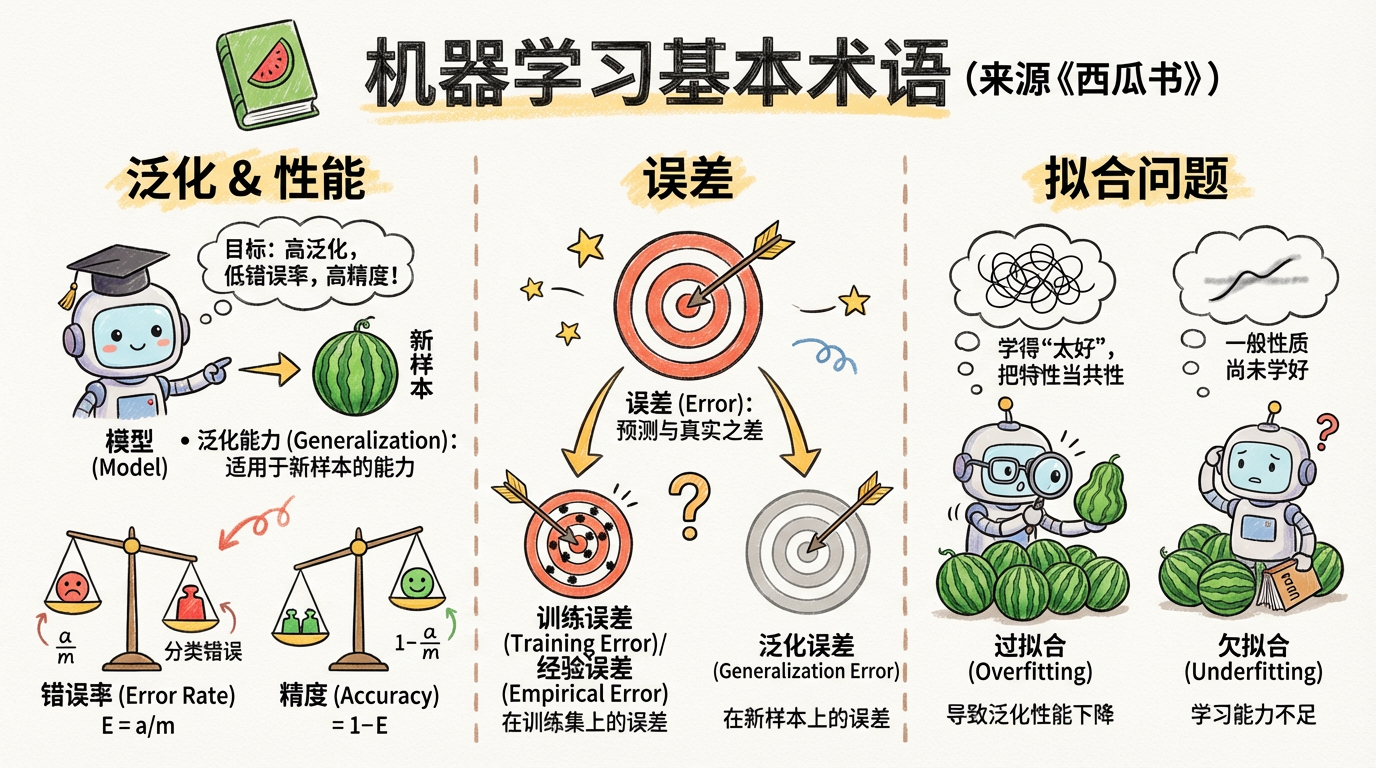
5 机器学习术语